An Optical Flow Based Left-Invariant Metric for Natural Gradient Descent in Affine Image Registration

D. J. Tward, in Frontiers in Applied Mathematics and Statistics

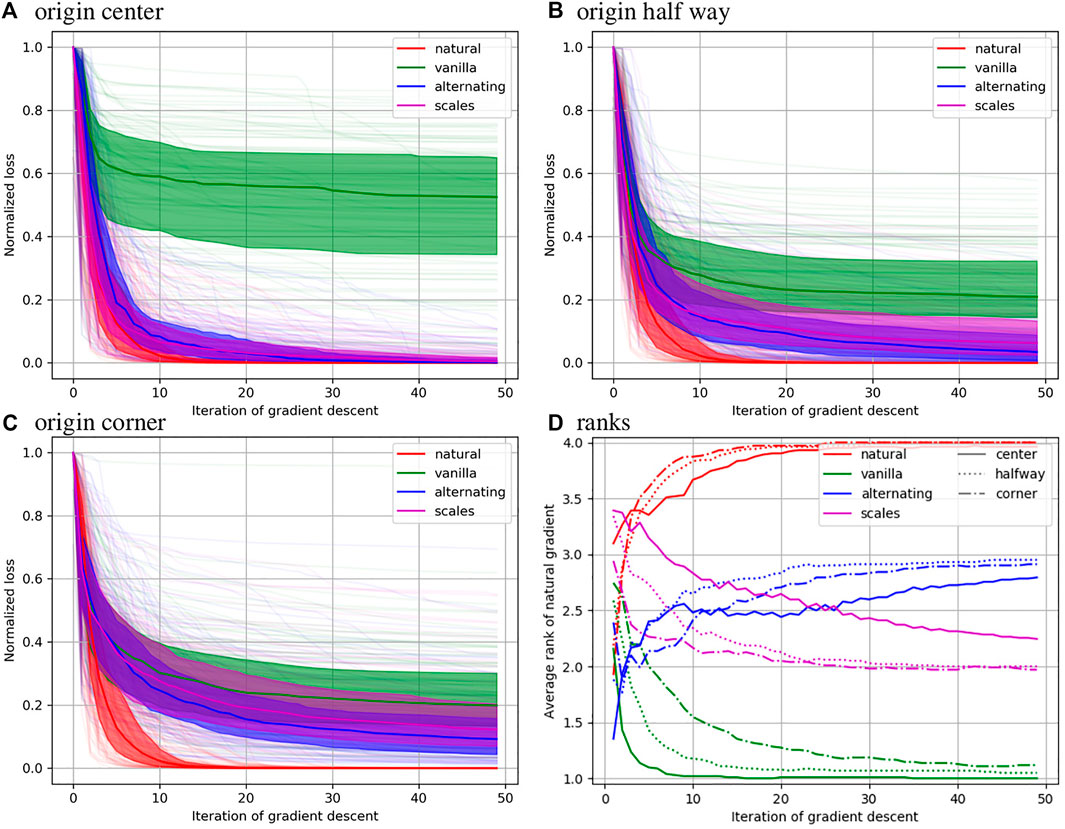
We developed a novel metric tensor for studying distances on the space of affine transformation matrices, and applied them to accelerate optimization in brain image alignment.

Accurate spatial alignment is essential for any population neuroimaging study, and affine (12 parameter linear/translation) or rigid (6 parameter rotation/translation) alignments play a major role. Here we consider intensity based alignment of neuroimages using gradient based optimization, which is a problem that continues to be important in many other areas of medical imaging and computer vision in general. A key challenge is robustness. Optimization often fails when transformations have components with different characteristic scales, such as linear versus translation parameters. Hand tuning or other scaling approaches have been used, but efficient automatic methods are essential for generalizing to new imaging modalities, to specimens of different sizes, and to big datasets where manual approaches are not feasible. To address this we develop a left invariant metric on these two matrix groups, based on the norm squared of optical flow induced on a template image. This metric is used in a natural gradient descent algorithm, where gradients (covectors) are converted to perturbations (vectors) by applying the inverse of the metric to define a search direction in which to update parameters. Using a publicly available magnetic resonance neuroimage database, we show that this approach outperforms several other gradient descent optimization strategies. Due to left invariance, our metric needs to only be computed once during optimization, and can therefore be implemented with negligible computation time.